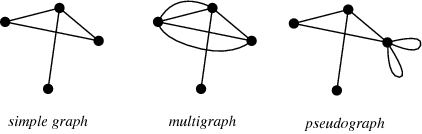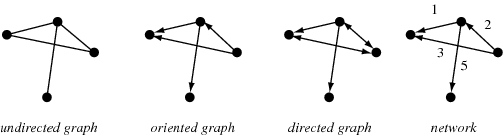
“The edges* of graphs* may… be imbued with directedness. A normal graph in which edges are undirected is said to be undirected. Otherwise, if arrows may be placed on one or both endpoints of the edges of a graph to indicate directedness, the graph is said to be directed. A directed graph in which each edge is given a unique direction (i.e., edges may not be bidirected and point in both directions at once) is called an oriented graph. A graph or directed graph together with a function which assigns a positive real number to each edge (i.e., an oriented edge-labeled graph) is known as a network.” (“Graph,” WolframMathWorld, retrieved 6/25/2020, including the picture).
.
*What is the Gist of a “Graph” (Graph Theory)?
.
Disclaimer:
I am not a professional in this field, nor do I claim to know all of the jargon that is typically used in this field. I am not summarizing my sources; I simply read from a variety of websites until I feel like I understand enough about a topic to move on to what I actually wanted to learn. By definition, none of these posts address every aspect of a topic. If I am inaccurate in what I say or you know a better, simpler way to explain a concept, I would be happy to hear from you :).